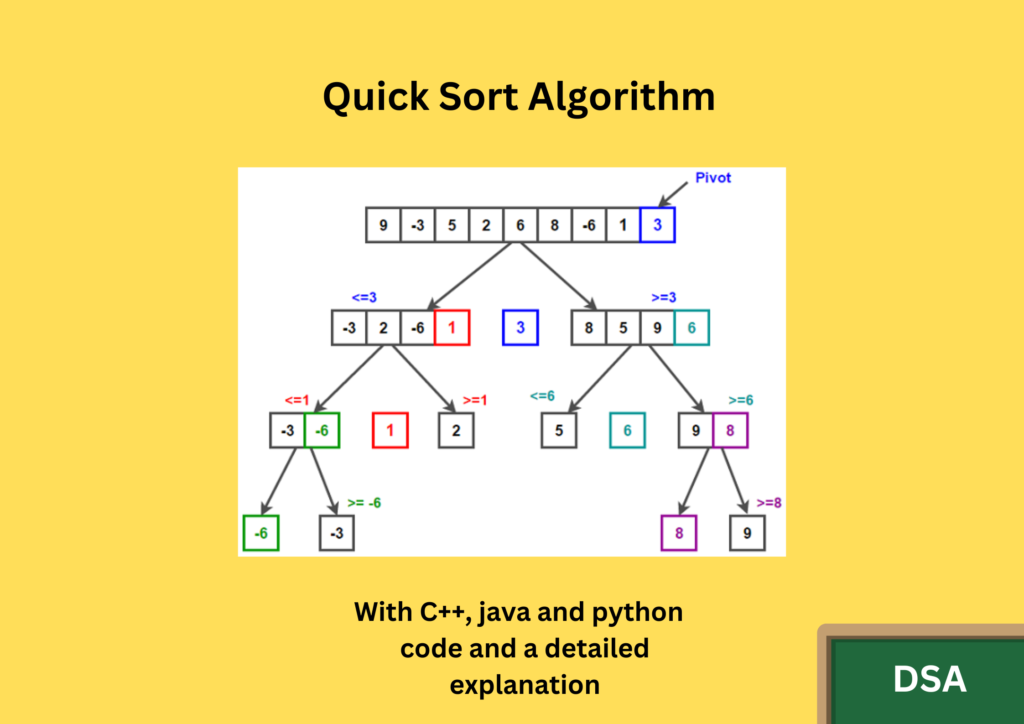
In this tutorial, we will learn about the Quick sort algorithm.
Sorting is one of the fundamental operations in computer science, and there are numerous sorting algorithms available. Merge sort is one such algorithm, which is efficient and widely used in programming languages. In this article, we will discuss the merge sort algorithm and its implementation in C++, Java, and Python.
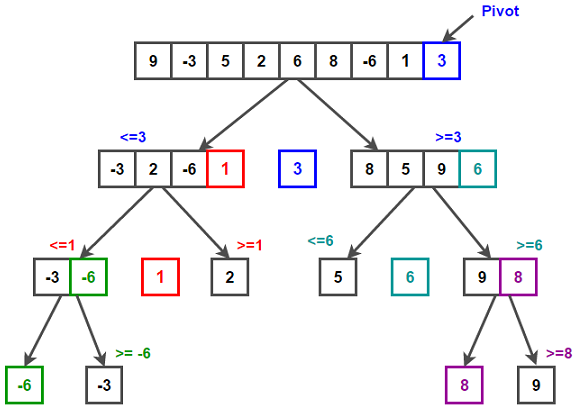
Quick Sort is a widely-used sorting algorithm that is often faster than other sorting algorithms for large data sets. It is a divide-and-conquer algorithm that works by partitioning an array into two parts, where the left side of the partition contains elements smaller than a pivot element and the right side contains elements larger than the pivot. The algorithm then recursively sorts the two partitions until the entire array is sorted. In this article, we will explore the Quick Sort algorithm with code examples in C++, Java, and Python.
C++ Implementation of Quick Sort:
#include<bits/stdc++.h>
using namespace std
void swap(int* a, int* b) {
int t = *a;
*a = *b;
*b = t;
}
int partition (int arr[], int low, int high) {
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j <= high- 1; j++) {
if (arr[j] < pivot) {
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
int main() {
int arr[] = {10, 7, 8, 9, 1, 5};
int n = sizeof(arr)/sizeof(arr[0]);
quickSort(arr, 0, n-1);
cout << "Sorted array: ";
for (int i=0; i < n; i++)
cout << arr[i] << " ";
return 0;
}
In the C++ implementation, the swap() function is used to swap two elements of an array. The partition() function selects the last element of the array as the pivot element and partitions the array into two parts. The quickSort() function recursively sorts the two partitions. In the main() function, we create an array, call the quickSort() function, and print the sorted array.
Java Implementation of Quick Sort:
static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
static int partition(int[] arr, int low, int high) {
int pivot = arr[high];
int i = low - 1;
for (int j = low; j < high; j++) {
if (arr[j] < pivot) {
i++;
swap(arr, i, j);
}
}
swap(arr, i + 1, high);
return i + 1;
}
static void quickSort(int[] arr, int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
public static void main(String[] args) {
int[] arr = {10, 7, 8, 9, 1, 5};
int n = arr.length;
quickSort(arr, 0, n - 1);
System.out.println("Sorted array: ");
for (int i = 0; i < n; i++) {
System.out.print(arr[i] + " ");
}
}
In java implementation, the swap() function is used to swap two elements of an array. The partition() function selects the last element of the array as the pivot element and partitions the array into two parts. The quickSort() function recursively sorts the two partitions. In the main() function, we create an array, call the quickSort() function, and print the sorted array.
Python Implementation of Quick Sort:
def swap(arr, i, j):
temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
def partition(arr, low, high):
pivot = arr[high]
i = low - 1
for j in range(low, high):
if arr[j] < pivot:
i += 1
swap(arr, i, j)
swap(arr, i + 1, high)
return i + 1
def quickSort(arr, low, high):
if low < high:
pi = partition(arr, low, high)
quickSort(arr, low, pi - 1)
quickSort(arr, pi + 1, high)
arr = [10, 7, 8, 9, 1, 5]
n = len(arr)
quickSort(arr, 0, n - 1)
print("Sorted array:")
for i in range(n):
print(arr[i], end=" ")
In the Python implementation, the swap() function is used to swap two elements of an array. The partition() function selects the last element of the array as the pivot element and partitions the array into two parts. The quickSort() function recursively sorts the two partitions. In the main() function, we create an array, call the quickSort() function, and print the sorted array.
Comparing each pass:
In each implementation, we can observe that the Quick Sort algorithm has an average time complexity of O(n*log n) and a worst-case time complexity of O(n^2). The algorithm performs better on average when compared to other sorting algorithms like Bubble Sort and Selection Sort.
In each pass of the algorithm, the pivot element is selected and the array is partitioned into two parts. The elements on the left side of the partition are smaller than the pivot element and the elements on the right side are larger than the pivot. The pivot element is then moved to its correct position in the array. The two partitions are then recursively sorted using the quickSort() function.
In the C++ and Java implementations, the swap() function is used to swap two elements of an array. However, in the Python implementation, we can directly swap two elements of an array without using a separate swap() function.
Conclusion
In conclusion, Quick Sort is a highly efficient sorting algorithm that can be used to sort large data sets. The algorithm has an average time complexity of O(n*log n) and performs better on average than other sorting algorithms. The C++, Java, and Python implementations of the algorithm are very similar and follow the same basic steps.