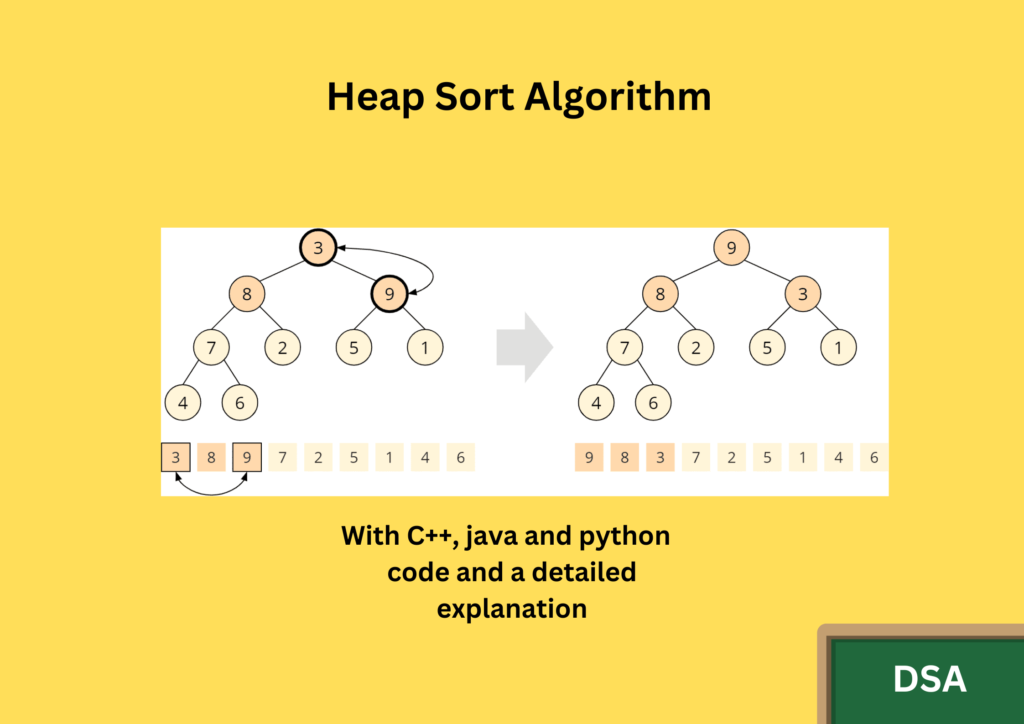
In this tutorial, we will learn about the Heap sort algorithm.
Sorting is one of the fundamental operations in computer science, and there are numerous sorting algorithms available. Merge sort is one such algorithm, which is efficient and widely used in programming languages. In this article, we will discuss the merge sort algorithm and its implementation in C++, Java, and Python.
Heap Sort is a comparison-based sorting algorithm that uses a binary heap data structure to sort an array in ascending or descending order. Heap Sort has a time complexity of O(n*log n), which makes it an efficient sorting algorithm for large datasets. In this article, we will explore the implementation of Heap Sort in C++, Java, and Python, along with an explanation of each pass of the algorithm.
C++ Implementation of Heap Sort:
void heapify(int arr[], int n, int i) {
int largest = i;
int l = 2*i + 1;
int r = 2*i + 2;
if (l < n && arr[l] > arr[largest])
largest = l;
if (r < n && arr[r] > arr[largest])
largest = r;
if (largest != i) {
swap(arr[i], arr[largest]);
heapify(arr, n, largest);
}
}
void heapSort(int arr[], int n) {
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
for (int i = n - 1; i >= 0; i--) {
swap(arr[0], arr[i]);
heapify(arr, i, 0);
}
}
int main() {
int arr[] = {12, 11, 13, 5, 6, 7};
int n = sizeof(arr)/sizeof(arr[0]);
heapSort(arr, n);
cout << "Sorted array is: \n";
for (int i = 0; i < n; ++i)
cout << arr[i] << " ";
}
In the C++ implementation, the heapify() function is used to create a heap from an array, and the heapSort() function is used to sort the array using the heap data structure. In the main() function, we create an array, call the heapSort() function, and print the sorted array.
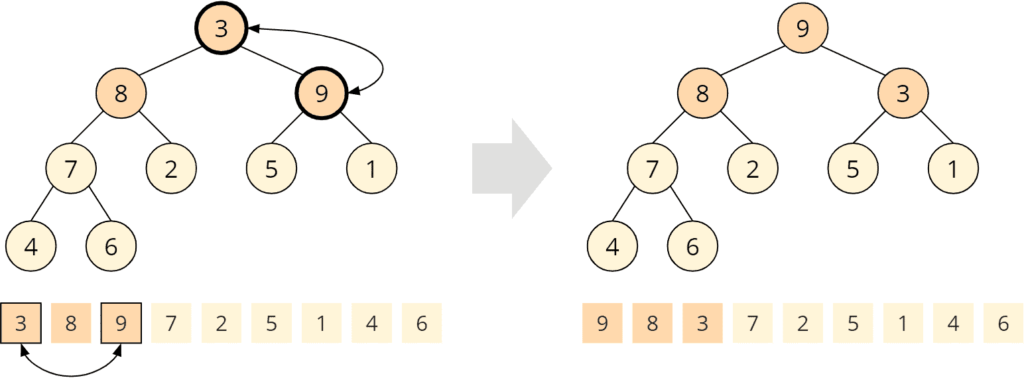
In the first pass of the algorithm, the heapify() function is called on each non-leaf node of the binary tree, starting from the bottom of the tree and working up to the root. The heapify() function compares the parent node with its left and right child nodes, and swaps the parent node with the largest child node if necessary. This creates a heap structure, where the largest element is at the root of the tree.
In the second pass of the algorithm, the heapSort() function repeatedly extracts the largest element from the root of the heap and places it at the end of the array. The heap is then reconstructed by calling heapify() on the remaining elements of the heap. This process continues until the entire array is sorted.
Java Implementation of Heap Sort:
Java Implementation of Heap Sort:
public class HeapSort {
public void sort(int arr[]) {
int n = arr.length;
// Build heap (rearrange array)
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
// One by one extract an element from heap
for (int i = n - 1; i >= 0; i--) {
// Move current root to end
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
// call max heapify on the reduced heap
heapify(arr, i, 0);
}
}
void heapify(int arr[], int n, int i) {
int largest = i; // Initialize largest as root
int l = 2 * i + 1; // left = 2*i + 1
int r = 2 * i + 2; // right = 2*i + 2
// If left child is larger than root
if (l < n && arr[l] > arr[largest])
largest = l;
// If right child is larger than largest so far
if (r < n && arr[r] > arr[largest])
largest = r;
// If largest is not root
if (largest != i) {
int swap = arr[i];
arr[i] = arr[largest];
arr[largest] = swap;
// Recursively heapify the affected sub-tree
heapify(arr, n, largest);
}
}
}
In the Java implementation, the HeapSort class has a sort() method that takes an array as input and sorts it using the heap sort algorithm. The heapify() method is used to create a heap from an array, and the sort() method calls the heapify() method on each non-leaf node of the binary tree to create a heap structure. The largest element is then repeatedly extracted from the root of the heap and placed at the end of the array, and the heap is reconstructed by calling heapify() on the remaining elements of the heap.
Python Implementation of Heap Sort:
def heapify(arr, n, i):
largest = i
l = 2 * i + 1
r = 2 * i + 2
if l < n and arr[i] < arr[l]:
largest = l
if r < n and arr[largest] < arr[r]:
largest = r
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)
def heapSort(arr):
n = len(arr)
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
for i in range(n - 1, 0, -1):
arr[0], arr[i] = arr[i], arr[0]
heapify(arr, i, 0)
arr = [12, 11, 13, 5, 6, 7]
heapSort(arr)
print("Sorted array is:")
for i in range(len(arr)):
print("%d" % arr[i])
The Python implementation of Heap Sort is similar to the C++ and Java implementations, with the heapify() function used to create a heap from an array, and the heapSort() function used to sort the array using the heap data structure. In the first pass of the algorithm, the heapify() function is called on each non-leaf node of the binary tree to create a heap structure. In the second pass of the algorithm, the largest element is repeatedly extracted from the root of the heap and placed at the end of the array, and the heap is reconstructed by calling heapify() on the remaining elements of the heap.
Each pass of the Heap Sort algorithm involves creating a heap from an array and then sorting the array using the heap data structure. In the first pass, the heapify() function is called on each non-leaf node of the binary tree to create a heap structure. In the second pass, the largest element is repeatedly extracted from the root of the heap and placed at the end of the array, and the heap is reconstructed by calling heapify() on the remaining elements of the heap.
Conclusion
In conclusion, Heap Sort is an efficient sorting algorithm with a time complexity of O(n*log n). It uses a binary heap data structure to sort an array in ascending or descending order. In this article, we explored the implementation of Heap Sort in C++, Java, and Python, along with an explanation of each pass of the algorithm. By understanding how Heap Sort works and how it can be implemented in various programming languages, developers can choose the best sorting algorithm for their applications and optimize their code for performance.