INTRODUCTION
In this tutorial, we are going to calculate the FIBONACCI SERIES USING RECURSION. Generally, the Fibonacci series is a type of series where the current number in the series is the sum of the two numbers that precede it. The Fibonacci series usually starts with 0 and 1. each number in the Fibonacci series is called a term.
For example, the first 10 terms of the Fibonacci series are as follows.
0 1 1 2 3 5 8 13 21 34
In the above series of numbers, after starting the series with 0 and 1, we see that the third element is the sum of its two precedents I.e. 0 and 1. and similarly until the 10th element. This is known as the Fibonacci series.
APPROACH 1
This is the basic approach for calculating the Fibonacci series. In this approach, we will calculate the value of each series by implementing a recursive call. In this, we will return the value of n itself if the value of n is less than or equal to 1, otherwise, we will return the sum of its two precedents.
ALGORITHM
Step 1: Start.
Step 2: recursive function will call itself until the value is greater than or equal to zero.
Step 3: until the value is lesser than or equal to 1, store the same value by using the above formula.
If n == 0 or n == 1 return n
else return (n-2)+(n-1)
Step 4: Stop.Below is the image representing the recursive calls of the Fibonacci series using recursion.
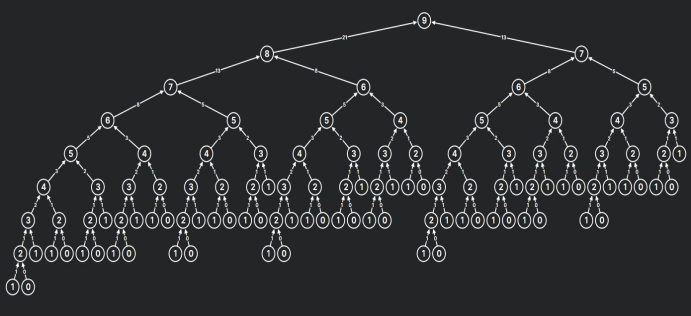
Let’s implement code for the Fibonacci series problem.
C++ Code:
#include <bits/stdc++.h>
using namespace std;
int fib(int n) {
if (n <= 1) return n;
else return fib(n - 1) + fib(n - 2);
}
int main() {
int n;
cin>>n;
cout<<"FIBONACCI SERIES IS : ";
for(int i = 0 ; i<n ; i++) cout<<fib(i)<<" ";
}
Python code:
def fib(n):
if n<=1:
return n
else:
return fib(n-2)+fib(n-1)
n = int(input())
print("FIBONACCI SERIES IS :",end=' ')
for i in range(n):
print(fib(i),end=' ')
JAVA code:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
int n = s.nextInt();
Fibonacci f = new Fibonacci();
System.out.print("FIBONACCI SERIES IS : ");
for(int i = 0 ; i<n ; i++) System.out.print(f.fib(i)+" ");
}
}
class Fibonacci{
public int fib(int n){
if (n <= 1) return n;
else return fib(n - 1) + fib(n - 2);
}
}
Input: 9
Output: FACTORIAL IS : 0 1 1 2 3 5 8 13 21 34
The time complexity of the code is O(2n), as every recursive function call splits into two recursive function calls.
The space complexity of the code is O(n), as we use a stack for storing each recursive call.As we can see in the above program, the time complexity will increase way too much for higher values of n as it will calculate the same value multiple times which will increase the redundancy and calculation time. What if stored the value of the recursive function, is once it is calculated? There is no need to calculate it again later it is called again, right? this process of storing the value of the recursively called function is known as memoization. The memory will increase some but the time complexity will decrease from O(2n) to O(N).
Let’s look at the recursive calls of the Fibonacci series problem using memoization.
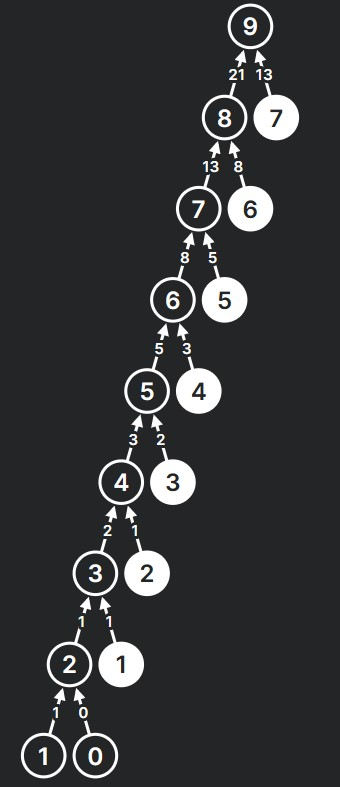
See! By using the memoization method the recursive calls which are previously calculated are stored somewhere else which makes us not calculate the recursive call value multiple times. Here, to store the recursive call value, we use an array to store the recursive function call values.
Let’s implement the code for the Fibonacci series problem using memoization.
C++ Code:
#include <bits/stdc++.h>
using namespace std;
int F[100];
int fib(int n) {
if (n <= 1) return n;
if(F[n] != -1) return F[n];
F[n] = fib(n-1)+fib(n-2);
return F[n];
}
int main() {
int n;
cin>>n;
for(int i = 0 ; i<100 ; i++) F[i]=-1;
cout<<"FIBONACCI SERIES IS : ";
for(int i = 0 ; i<n ; i++) cout<<fib(i)<<" ";
}
Python code:
F=[-1 for i in range(100)]
def fib(n):
if n<=1:
return n
if F[n] != -1:
return F[n]
JAVA code:
import java.util.*;
public class Main {
static int F[] = new int[100];
static int fib(int n){
if (n <= 1) return n;
if(F[n] != -1) return F[n];
F[n] = fib(n-1)+fib(n-2);
return F[n];
}
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
int n = s.nextInt();
for(int i = 0 ; i<100 ; i++) F[i]=-1;
System.out.print("FIBONACCI SERIES IS : ");
for(int i = 0 ; i<n ; i++) System.out.print(fib(i)+" ");
}
}
Conclusion
That’s it from this tutorial. Hope you guys found It interesting. We have solved the Fibonacci series program and memoization of the Fibonacci series problem in different programming languages. Happy coding!

