INTRODUCTION
In this tutorial, we will learn about the Merge SORT ALGORITHM.
Sorting is one of the fundamental operations in computer science, and there are numerous sorting algorithms available. Merge sort is one such algorithm, which is efficient and widely used in programming languages. In this article, we will discuss the merge sort algorithm and its implementation in C++, Java, and Python.
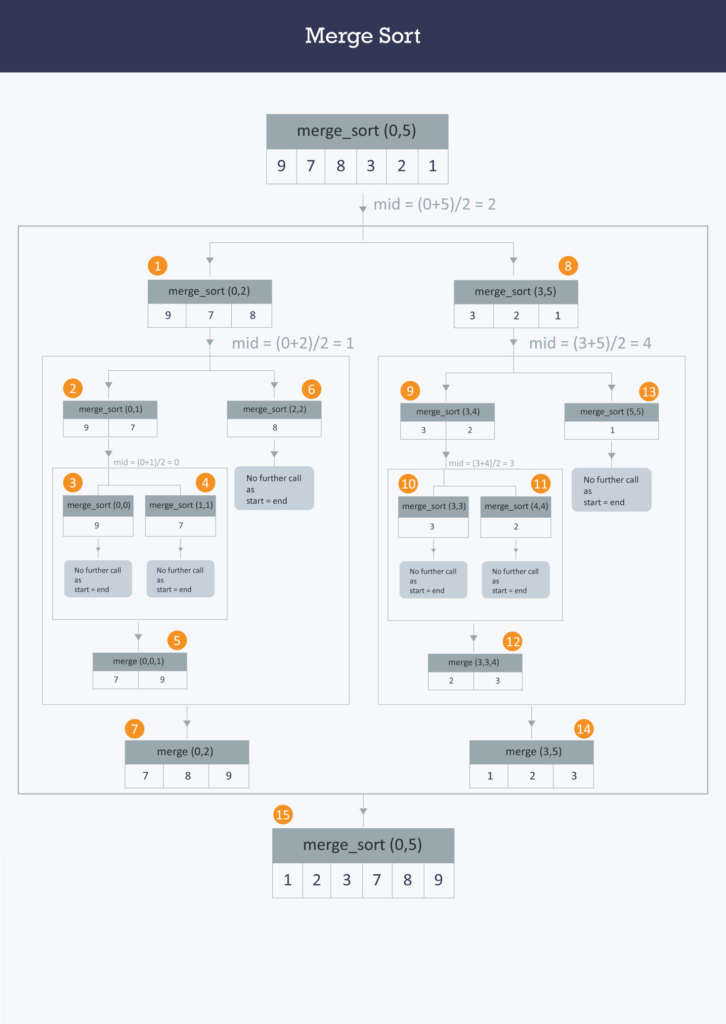
Merge sort is a divide-and-conquer algorithm that sorts an array by dividing it into two halves, sorting each half, and then merging the two halves. It is a stable sorting algorithm, meaning that it maintains the relative order of equal elements. Merge sort has a time complexity of O(nlogn), where n is the number of elements to be sorted.
The merge sort algorithm can be divided into two main steps: the divide step and the merge step. In the divide step, the array is divided into two halves, and each half is sorted recursively using merge sort. In the merge step, the two sorted halves are merged to produce the final sorted array.
Now let’s see the implementation of the merge sort algorithm in C++, Java, and Python.
C++ Implementation:
#include <iostream>
using namespace std;
void merge(int arr[], int l, int m, int r)
{
int n1 = m - l + 1;
int n2 = r - m;
int L[n1], R[n2];
for (int i = 0; i < n1; i++)
L[i] = arr[l + i];
for (int j = 0; j < n2; j++)
R[j] = arr[m + 1 + j];
int i = 0, j = 0, k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
}
else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
void mergeSort(int arr[], int l, int r)
{
if (l < r) {
int m = l + (r - l) / 2;
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
merge(arr, l, m, r);
}
}
int main()
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
int arr_size = sizeof(arr) / sizeof(arr[0]);
mergeSort(arr, 0, arr_size - 1);
cout << "Sorted array: \n";
for (int i = 0; i < arr_size; i++)
cout << arr[i] << " ";
return 0;
}
In the above C++ code, the merge() function takes three parameters: the array, the starting index of the first subarray, the ending index of the first subarray, and the ending index of the second subarray. The function first copies the elements of the two subarrays into two separate arrays, L and R, and then merges the two arrays into the original array arr. The mergeSort() the function is the main function that calls itself recursively to sort the array.
Java Implementation:
class MergeSort {
void merge(int arr[], int l, int m, int r)
{
int n1 = m - l + 1;
int n2 = r - m + 1;
int L[] = new int[n1];
int R[] = new int[n2];
for (int i = 0; i < n1; ++i)
L[i] = arr[l + i];
for (int j = 0; j < n2; ++j)
R[j] = arr[m + 1 + j];
int i = 0, j = 0;
int k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
}
else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
void mergeSort(int arr[], int l, int r)
{
if (l < r) {
int m = (l + r) / 2;
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
merge(arr, l, m, r);
}
}
public static void main(String args[])
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
int arr_size = arr.length;
MergeSort ob = new MergeSort();
ob.mergeSort(arr, 0, arr_size - 1);
System.out.println("Sorted array:");
for (int i = 0; i < arr_size; ++i)
System.out.print(arr[i] + " ");
}
}
In the above Java code, the merge() function is similar to the C++ code. The mergeSort() function is the main function that calls itself recursively to sort the array. In the main() function, we create an object of the MergeSort class and call the mergeSort() function to sort the array.
Python Implementation:
def merge(arr, l, m, r):
n1 = m - l + 1
n2 = r- m
L = [0] * (n1)
R = [0] * (n2)
for i in range(0, n1):
L[i] = arr[l + i]
for j in range(0, n2):
R[j] = arr[m + 1 + j]
i = 0
j = 0
k = l
while i < n1 and j < n2:
if L[i] <= R[j]:
arr[k] = L[i]
i += 1
else:
arr[k] = R[j]
j += 1
k += 1
while i < n1:
arr[k] = L[i]
i += 1
k += 1
while j < n2:
arr[k] = R[j]
j += 1
k += 1
def mergeSort(arr, l, r):
if l < r:
m = (l+(r-1))//2
mergeSort(arr, l, m)
mergeSort(arr, m+1, r)
merge(arr, l, m, r)
arr = [12, 11, 13, 5, 6, 7]
n = len(arr)
mergeSort(arr, 0, n-1)
print("Sorted array:")
for i in range(n):
print(arr[i], end=" ")
In the above Python code, the merge() function is the same as the C++ and Java code. The mergeSort() function is the main function that calls itself recursively to sort the array. In the main() function, we create an array and call the mergeSort() function to sort the array. Finally, we print the sorted array using a for loop.
In the above Python code, the mergeSort() function takes an array as input and recursively sorts the array by dividing it into two halves. The merge() step is similar to the C++ and Java code. In the main() function, we create an array and call the mergeSort() function to sort the array.
Conclusion:
In this article, we discussed the merge sort algorithm and its implementation in C++, Java, and Python. Merge sort is a fast and efficient sorting algorithm with a time complexity.


