INTRODUCTION
In this tutorial, we are going to learn about different kinds of problem-solving approaches that are used for solving problems in data structures and algorithms. Learning these strategies will be helpful to master the data structures and algorithms.
Let’s look at some popular PROBLEM-SOLVING APPROACHES IN DATA STRUCTURES AND ALGORITHMS.

These are some of the popular problem-solving strategies used to solve problems in data structures and algorithms. Let’s take a look at each.
Divide and conquer algorithm:
divide and conquer is a popular problem-solving approach used in solving problems in data structures where we tend to divide the whole problem into more than one sub-problem, and if needed we can combine the solutions of the sub-problems to get the solution for the original problem. This approach is known as the divide and conquer algorithm. This approach is used to solve the sub-problems parallelly by using multi-processing.

Note: as this approach uses recursion in solving the problem, sometimes it may be slow in compiling the solution of each sub-problem. In case the logic is missed anywhere during solving the problem, the recursion may occur rigorously and it may crash the computer.
Problem-solving using data structures:
using data structures, we can increase the efficiency of solving problems greatly by using some of the critical operations and functions. There are different kinds of data structures available to solve the given problem efficiently.
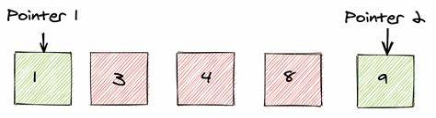
Two-pointers algorithm:
two pointers algorithm is a pair of array indices or pointers references to an object. This approach helps us to optimize time and space complexity by simultaneously iterating over to different input parts to perform operations according to the problem. This two-pointer approach is performed on the array which follows some specific order.
Dynamic programming:
dynamic programming approach dynamic programming is one of the most popular approaches for solving problems with overlapping and repeating sub-problems. In this approach, instead of solving overlapping sub-problems repeatedly, we solve the sub-problem only once and we store the result of the sub-problem in the main memory. Problems regarding optimization and counting problems can be solved efficiently by using this approach.
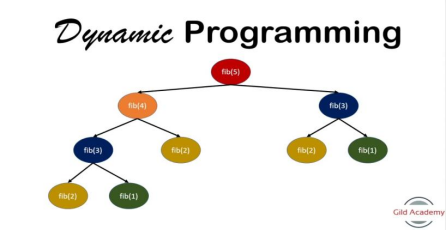
Note: this approach applies only when the sub-problems are dependent and repeated during recursive calls.
Greedy approach:
In the greedy approach, we choose the best optimal solution among the group of solutions that are available at that moment. By using the greedy approach, we can only find the best optimal solution among the group of solutions available at that moment and not focus on whether the entire solution at the end would be optimal or not. This technique is usually used to obtain a feasible solution rather than thinking about whether the optimal solution is obtained or not.

Exhaustive approach:
In this approach, we have to find all the possible solutions to the problem until the solution to the problem is found. Finding all the possible solutions for the given problem, increases the time complexity and space in some cases, making it more inefficient. But in some cases, it is necessary to find all the possible solutions for the given problem. Hence, this approach is rarely offered to a person to solve a problem by using this strategy.
Backtracking:
Backtracking is a method in which we generate solutions by avoiding unnecessary possibilities. Backtracking is better than an exhaustive approach in the case of efficiency as we avoid some solutions which are not necessary. In simple words, backtracking is generally a trial-and-error methodology that involves not to do wrong choices by checking them. When the number of trials decreases, the efficiency of the problem increases. This is known as backtracking.
CONCLUSION
That’s it from this tutorial. Hope you guys found it interesting. We have learned about different kinds of problem-solving approaches in data structures. Happy coding!

