INTRODUCTION
In this tutorial, we are going to learn about a popular search algorithm, Linear Search in DSA.
linear search. The linear search follows a sequential order in which searching for an element in an array starts from one end and continues to traverse towards another end of the array till the desired element is found. If the desired element is not found, then the search is continued till the last element of the array.
Let’s take a look at the pictorial representation of the linear search algorithm.
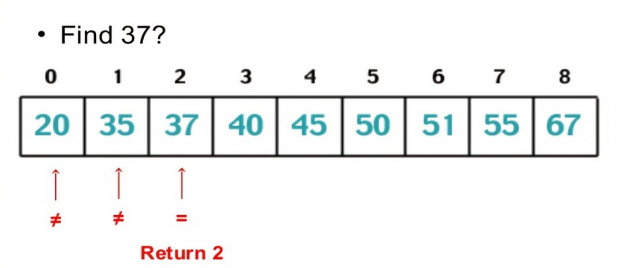
In the above example, the iteration starts from the 0th index and checks till 37 is found. After finding 37, it returns the index of 37.
APPROACH 1
This is a normal approach in which we iterate the loop from the first element of the array and if the target element is found anywhere during iteration, return the index, or else iterate the loop till the last element of the array.
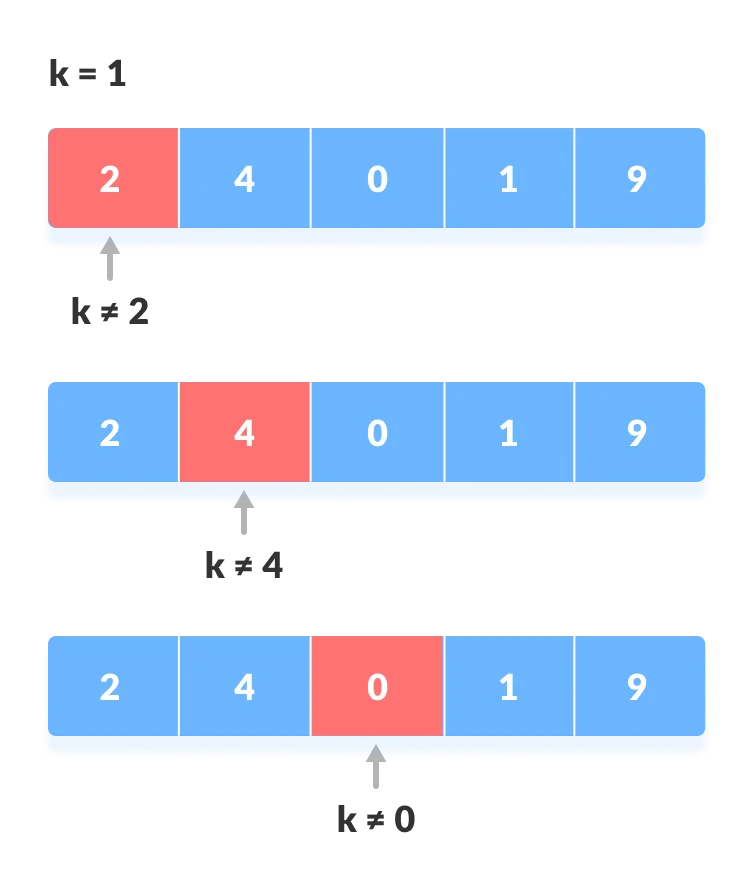
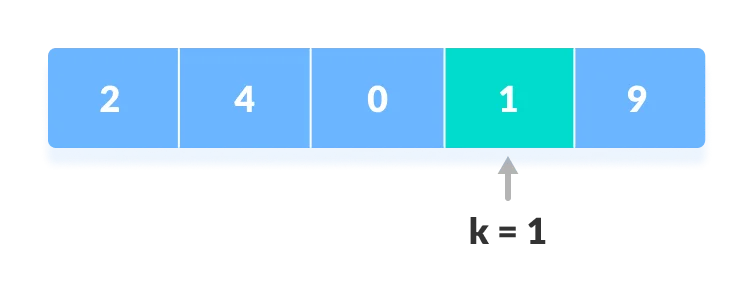
ALGORITHM
Step 1: start.
Step 2: Start the iteration from the first element of the array. Initialize zero to a temporary variable “flag”.
Step 3: if the desired element is found at a particular position, then return the index and set flag =1, or else iterate till the last element of the array.
Step 4: if the flag value equals zero, it means the target element is not present in the array and returns the message “key not found”.
Step 5: Stop.C++ Code:
#include <iostream>
using namespace std;
int main() {
int n,key,temp=0;
cin>>n;
int a[n];
for(int i = 0 ; i<n ; i++) cin>>a[i];
cin>>key;
for(int i = 0 ; i<n ; i++)
if(a[i] == key) {
cout<<i;
temp=1;
}
if(temp == 0) cout<<"KEY NOT FOUND";
}
Python code:
size = int(input())
l = []
for i in range(size):
x = int(input())
l.append(x)
key = int(input())
for i in range(size):
if l[i] == key:
print(i)
break
else:
print("KEY NOT FOUND")
JAVA code:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
int size = s.nextInt();
int a[];
a = new int[5];
int temp=0;
for(int i = 0 ; i<size ; i++) a[i] = s.nextInt();
int key = s.nextInt();
for(int i = 0 ; i<size ; i++)
if(a[i] == key){
System.out.println(i);
temp=1;
}
if (temp == 0) System.out.println("KEY NOT FOUND");
}
}
Input: 5
1 2 3 4 5
5
Output: 4
The time complexity of the code is O(n) as here we use a for loop.
The space complexity of the code is O(1).Approach 2
In the recursive method, we check the last element of the array with the target element and we recursively call the function by decreasing the size of the element.
ALGORITHM
Step 1: Start.
Step 2: Check the last element of the array is equal to the target element or not. If the last element is equal to the target element, then return size-1.
Step 3: If the size of the array equals zero, it means the target element is not present in the array.
Step 4: Stop.C++ Code:
#include <iostream>
using namespace std;
int linearsearch(int a[], int size, int key){
if(a[size-1] == key) return size-1;
else if (size == 0 ) return -1;
else return linearsearch(a,size-1,key);
}
int main() {
int n,key;
cin>>n;
int a[n];
for(int i = 0 ; i<n ; i++) cin>>a[i];
cin>>key;
cout<<linearsearch(a,n,key);
}
Python code:
def linearsearch(l,size,key):
if l[size-1] == key:
return size-1
elif size == 0:
return -1
else:
return linearsearch(l,size-1,key)
size = int(input())
l = []
for i in range(size):
x = int(input())
l.append(x)
key = int(input())
print(linearsearch(l,size,key))
JAVA code:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
int size = s.nextInt();
int a[];
a = new int[5];
int temp=0;
for(int i = 0 ; i<size ; i++) a[i] = s.nextInt();
int key = s.nextInt();
LinearSearch l = new LinearSearch();
System.out.println(l.linearsearch(a,size,key));
}
}
class LinearSearch {
int linearsearch(int a[], int size, int key){
if(a[size-1] == key) return size-1;
else if (size == 0 ) return -1;
else return linearsearch(a,size-1,key);
}
}
Input: 5
1 2 3 4 5
5
Output: 4
The time complexity of the code is O(n) as here we use a for loop.
The space complexity of the code is O(n), as we use a stack for storing each recursive call.Now let’s look at some of the advantages of the linear search
- The linear search algorithm is simple and easy to understand.
- We can implement linear search in an unordered list of elements also.
- Extra space is not required for linear search.
Now let’s look at some of the disadvantages of the linear search
- The time complexity of the linear search algorithm is O(n), which makes it slow when compared with other search algorithms.
- The linear search algorithm is not suitable for a large data set of elements.
- The linear search algorithm is recommendable if the size of the data set is comparatively small.
Conclusion
That’s it from this tutorial. Hope you guys found It interesting. We have solved the linear search algorithm in different programming languages. Happy coding!

