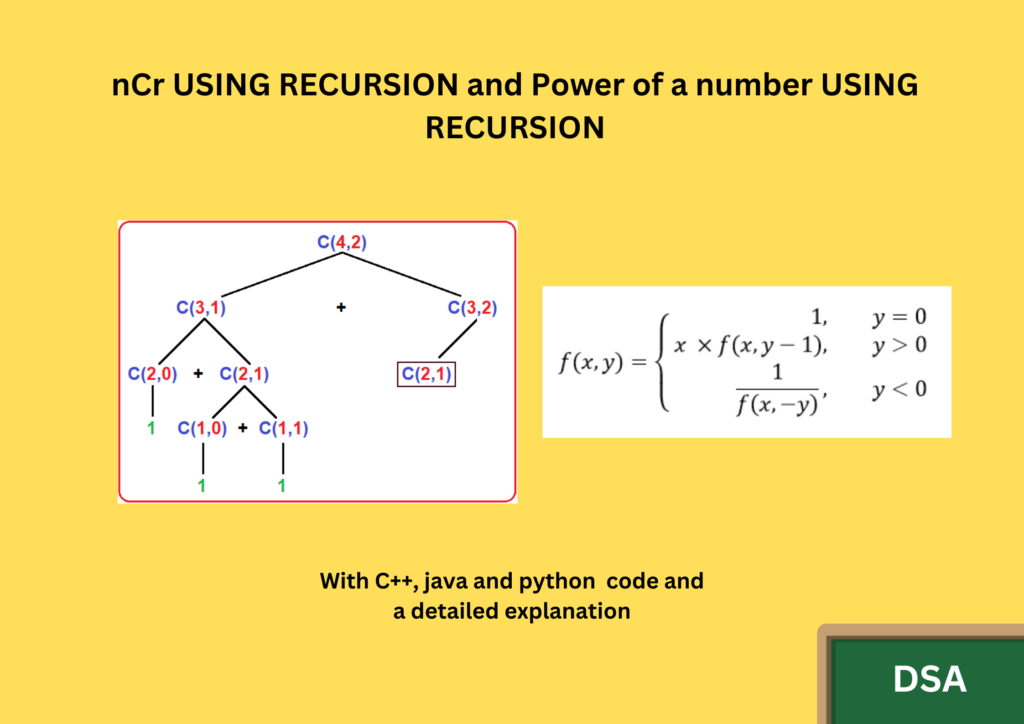
In this article, we are going to have a look at nCr USING RECURSION and POWER OF A NUMBER USING RECURSION.
INTRODUCTION: nCr USING RECURSION
In this tutorial, we are going to calculate the combination formula, nCr using recursion
The nCr is a combination that is known for the selection of things without considering the order of the arrangement. This formula is used to find the possible arrangements where a selection of things is done without consideration of the order.
For example:
Input n = 5 r = 2
Output: 10.
APPROACH 1
In this tutorial, we are going to calculate the combination formula, nCr using recursion
The nCr is a combination that is known for the selection of things without considering the order of the arrangement. This formula is used to find the possible arrangements where a selection of things is done without the consideration of the order.
For example:
Input n = 5 r = 2
Output: 10.
ALGORITHM
Step 1: Start.
Step 2: recursive function will call itself until the value of r is lesser than n.
Step 3: until the base condition of the function is satisfied, we will recursively call the function and store the returned value. The base condition of the function is.
If r==0 or r==n return 1
If n<r return 0
Else return (n - 1, r - 1) + (n - 1, r)
Step 4: Stop.C++ Code:
#include <iostream>
using namespace std;
int nCr(int n, int r) {
if (r > n) return 0;
if (r == 0 || r == n) return 1;
return nCr(n - 1, r - 1) + nCr(n - 1, r);
}
int main() {
int n,r;
cin>>n>>r;
int NCR = nCr(n,r);
cout<<NCR;
}
Python code:
def nCr(n,r):
if r==0 or r==n:
return 1
if n<r:
return 0
return nCr(n - 1, r - 1) + nCr(n - 1, r)
n = int(input())
r = int(input())
print(nCr(n,r))
JAVA code:
import java.util.*;
public class Main {
static int nCr(int n, int r) {
if (r > n) return 0;
if (r == 0 || r == n) return 1;
return nCr(n - 1, r - 1) + nCr(n - 1, r);
}
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
int n = s.nextInt();
int r = s.nextInt();
int NCR = nCr(n,r);
System.out.println(NCR);
}
}
Input: 5 2
Output: 10
The time complexity of the code is O(2n).
The space complexity of the code is O(N2).INTRODUCTION: POWER OF A NUMBER USING RECURSION
In this tutorial, we are going to calculate the fPOWER OF A NUMBER USING RECURSION.
Given an integer N, write a program to calculate the power of a number using recursion.
Ex1:
Input : base=2 and power=2
Output: 4
Ex2:
Input N: base=2 and power=3
Output: 8
APPROACH 1
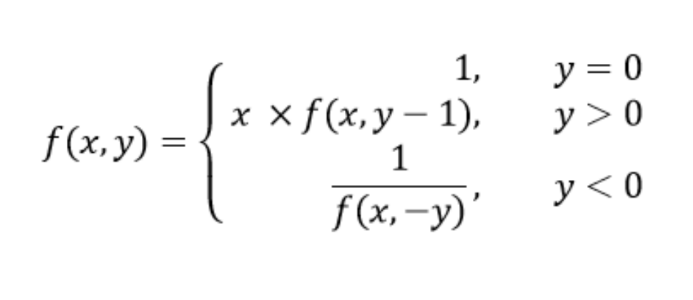
We will transform the above mathematical function as follows:
- First, give a meaningful name to our recursive function say power()
2. The function must accept two numbers i.e., base and expo, and calculate its power. Hence, take two parameters for base and exponent, say power(int base, int expo);
LOGIC
Logic to calculate the power of a number using recursion
After declaring the pow() function it’s time to define logic to find power recursively. There can be three cases while calculating the power of a number.
- If the exponent is 0, then the power is 1. This is the base condition of our recursive function.
- If the exponent is negative, then the power is 1 / (x ^ -y). Which uses a recursive call to the pow() function for computing the value of (x ^ -1) i.e. 1 / pow(base, -expo).
- If the exponent is positive, then calculate power normally using x ^ y. Computing x ^ y also makes a recursive call i.e. base * pow(base, expo – 1)
Let us combine all three conditions in a single recursive function.
ALGORITHM
STEP-1:Start
STEP-2: take input base,exponent
STEP-3: Base condition of recursion:A*o=1;(anything to the power of 0 is 1).
STEP-4: To calculate An ,we can first calculate A*n-1 and then multiply it with A(A*n=A x A*n-1) and store it in result
STEP-5:Stop.C++ Code:
#include <iostream>
using namespace std;
int power(int base, int expo){
if(expo == 0) return 1;
else return base*power(base,expo-1);
}
int main()
{
int base,expo;
cout<<"enter base and exponent values: ";
cin>>base>>expo;
cout<<"result is: "<<power(base,expo);
}
Python code:
def power(base,expo):
if expo==0:
return 1
elif expo>0:
return base*power(base,expo-1)
else:
return 1/power(base,-exponent)
base=int(input("enter the number"))
expo=int(input("enter power of a number"))
result=power(base,expo)
print(result)
JAVA code:
import java.util.*;
public class Basic
{
public static void main(String[] args){
Scanner reader =new Scanner(System.in);
int base =reader.nextInt();
System.out.println("enter power:");
int expo=reader.nextInt();
int result=power(base,expo);
System.out.println("power of number is:"+result);
}
public static int power(int base,int expo)
{
if(expo==0){
return 1;
}
else{
return base*power(base,expo-1);
}
}
}
OUTPUT:
Enter base:
3
enter power:
2
power of number is:9
TIME COMPLEXITY OF THE CODE IS: O(n)CONCLUSION
CONCLUSION
That’s it from this tutorial. Hope you guys found it interesting. We have solved the ncr and the power of a number in different programming languages. Happy coding!