In this article, we are going to learn about RECURSION AND ITS TYPES in a detailed way.
RECURSION:
The process in which a function calls itself directly or indirectly is called recursion and the corresponding function is called a recursive function. Using the recursive algorithm we can solve problems such as Towers of Hanoi, Inorder/Preorder/Postorder Tree Traversals, DFS of Graph, etc. . The recursion function follows the LAST IN FIRST OUT structure.
PROS OF RECURSION:
It reduces the time complexity
It is better at tree traversal
It makes it easier to read and write
Helps in solving data structure problems.
CONS OF RECURSION:
It requires lots of memory
sometimes difficult to analyze code
sometimes it can be slow
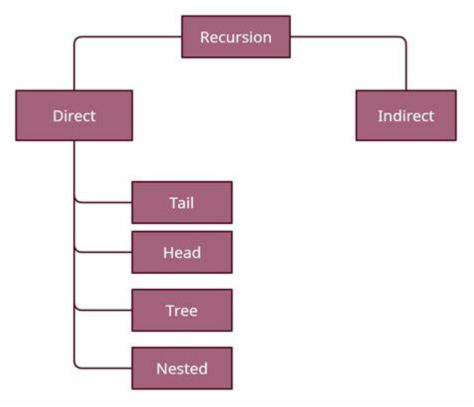
TYPES OF RECURSION:
- Tail Recursion
- Head Recursion
- Tree Recursion
- Indirect Recursion
- Nested Recursion
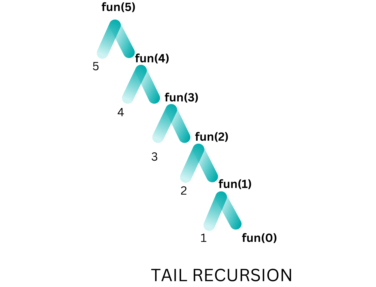
TAIL RECURSION:
Tail recursion is the recursive function in which the recursive call is the last statement that is executed by the function. Nothing is left to execute after the recursion call. Tail recursion is better than non-tail recursive functions. Because Tail recursion is optimized by the compiler. whenever we call the function its address is stored inside the stack.
Time Complexity for Tail Recursion: O(n)
Space Complexity for Tail Recursion: O(n)
EXAMPLE PROGRAMS
C++:
#include <iostream>
using namespace std;
// Recursion function
void fun(int n)
{
if (n > 0) {
cout << n << " ";
// Last statement in the function
fun(n - 1);
}
}
int main()
{
int c = 5;
fun(c);
return 0;
}
OUTPUT:
5 4 3 2 1HEAD RECURSION:
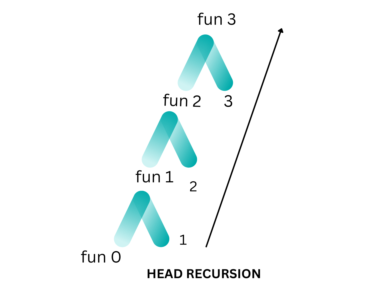
If a recursive function calls itself and that recursive call is the first statement in the function then it’s known as Head Recursion. There’s no statement, and no operation before the call. The function doesn’t have to process or perform any operation at the time of calling and all operations are done at returning time.
Time Complexity For Head Recursion: O(n)
Space Complexity For Head Recursion: O(n)
EXAMPLE PROGRAMS:
C++
#include "bits/stdc++.h"
using namespace std;
// Recursive function
void fun(int n)
{
if (n > 0) {
// First statement in the function
fun(n - 1);
cout << " "<< n;
}
}
// Driver code
int main()
{
int x = 3;
fun(x);
return 0;
}
OUTPUT:
5 4 3 2 1TREE RECURSION:
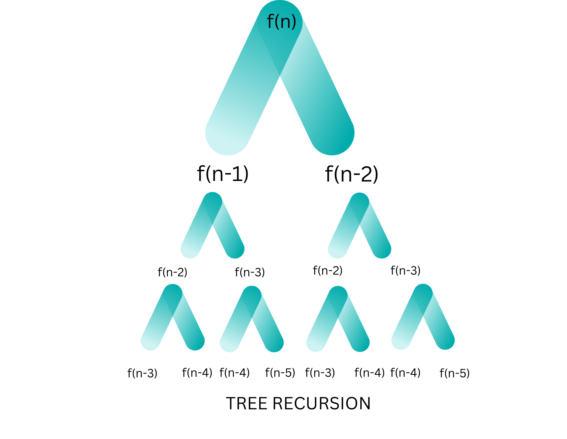
To understand Tree Recursion let’s first understand Linear Recursion. If a recursive function calls itself for one time then it’s known as Linear Recursion. if a recursive function calls itself more than one time then we call it a Tree Recursion.
Time Complexity For Tree Recursion: O(2^n)
Space Complexity For Tree Recursion: O(n)
EXAMPLE PROGRAMS FOR TREE RECURSION:
C++
#include <iostream>
using namespace std;
void fun(int n)
{
if (n > 0)
{
cout << " " << n;
fun(n - 1);
fun(n - 1);
}
}
// Driver code
int main()
{
fun(3);
return 0;
}
OUTPUT:
3 2 1 1 2 1 1NESTED RECURSION:
In this recursion, a recursive function will pass the parameter as a recursive call. It means the recursion inside the recursion. Let’s see the example to understand this recursion.
Time Complexity For Tree Recursion: O(2^n)
Space Complexity For Tree Recursion: O(n)

EXAMPLE PROGRAMS FOR NESTED RECURSION:
C++
#include <iostream>
using namespace std;
int fun(int n)
{
if (n > 100)
return n - 10;
return fun(fun(n + 11));
}
int main()
{
int r;
r = fun(95);
cout << " " << r;
return 0;
}
OUTPUT:
91INDIRECT RECURSION:
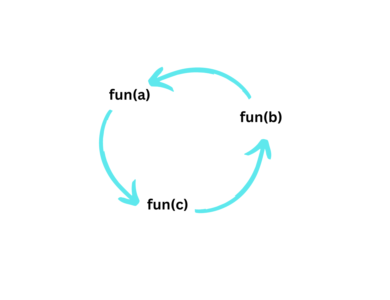
In this recursion, there may be more than one function and they are circularly calling one another.
From the below diagram, fun(A) is calling for fun(B), fun(B) is calling for fun(C) and fun(C) is calling for fun(A) and thus it makes a cycle.
EXAMPLE FOR INDIRECT RECURSION:
C++
#include <iostream>
using namespace std;
void funB(int n);
void funA(int n)
{
if (n > 0) {
cout <<" "<< n;
// fun(A) is calling fun(B)
funB(n - 1);
}
}
void funB(int n)
{
if (n > 1) {
cout <<" "<< n;
funA(n / 2);
}
}
int main()
{
funA(20);
return 0;
}
Output:
20 19 9 8 4 3 1
