INTRODUCTION
In this tutorial, we will learn about RECURSION IN DSA, various kinds of recursive functions, and their properties. Now first of all, what is meant by recursion?
Recursion is a process in which a function calls itself directly or indirectly until the base condition of the recursive function breaks. In recursion, the approach solves a particular problem by calling the same function again and dividing the main problem into smaller sub-problems. We can call the recursive function according to the problem.
void recursion(){
recursion();
}
int main() {
recursion();
}This is what a recursive function looks like.
A recursive function can call itself infinitely. To avoid infinite running, the recursive function should possess two properties.
Base criteria: there must be at least one base condition, such that when this condition breaks, the function should stop calling itself, otherwise stack overflow problems may arise.
Progressive approach: the approach of the recursion should be in a way that, each time a recursive call is made, it comes closer to the base criteria.
These are the two properties that should be followed to avoid the infinite running of a recursive function.
Now we have basic knowledge about recursion, for what purpose it is used?
Now, we will learn about the need for recursion in programming and problem-solving.
- By using recursion, the length of the code is reduced.
- The readability and re-usability of the code will be increased.
- Recursion will be the best approach to solve a problem where a problem is defined by solving with a similar sub-problem.
- Recursion provides a clean and simple way to write the code.
Now let’s look at some of the disadvantages of implementing recursion in problem-solving.
- The recursive approach of problem-solving occupies greater space than the iterative approach.
- As the function calls itself and returns, time complexity also increases in some cases.
- If the base condition is not mentioned properly, the computer may run out of memory.
- As the size of the code decreases, debugging every function call needs extra care for understanding.
These are some of the disadvantages of recursion.
Now we will get confused that what are the main differences between recursion and iteration. Let’s look at the main differences between iteration and recursion.
Differences between recursion and iteration
| RECURSION | ITERATION |
| Recursion is a process of function calling itself. | Iteration is the process of executing a set of instructions repetitively until the condition is false. |
| Termination of the base condition of the code is defined within the recursive function. | Termination of the condition is defined in the definition of the loop. |
| Recursion is applied to functions. | Iteration is applied to loops. |
| Recursion is slower when compared with iteration. | Iteration is faster when compared with recursion. |
| Recursion has high time and space complexity when compared with iteration. | Iteration has less time and space complexity when compared with recursion. |
| The size of the code using recursion is smaller. | The size of the code using iteration is big when compared with recursion. |
| In recursion, there is an extensive overhead. | In iteration, there is no overhead. |
Now let’s look at the working of the recursion
As we know, recursion is the process of a function calling itself until the base condition achieves. After the base condition breaks, the function call stops. Let’s understand the working of the recursion with an example.
If we look at the factorial function, we will perform the required number of the recursive call to the function. Let’s look at a sample example.
5*factorial(4) // 5*factorial(4)
4*factorial(3) // 5*4*factorial(3)
3*factorial(2) // 5*4*3*factorial(2)
2*factorial(1) // 5*4*3*2*factorial(1)
1*factorial(0) // 5*4*3*2*1*factorial(0)Let’s look at the sample program implementing the factorial function.
C++ Code:
#include <iostream>
using namespace std;
int factorial(int n){
if( n == 1 || n == 0) return 1;
else return n*factorial(n-1);
}
int main() {
int n;
cin>>n;
cout<<"FACTORIAL IS : "<<factorial(n);
}
Python code:
def factorial(n):
if n == 0 or n == 1:
return 1
else:
return n*factorial(n-1)
n = int(input())
print("FACTORIAL IS :",factorial(n))
JAVA code:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
Factorial f = new Factorial();
int n = s.nextInt();
System.out.println("FACTORIAL IS : "+f.factorial(n));
}
}
class Factorial {
int factorial(int n){
if( n == 1 || n == 0) return 1;
else return n*factorial(n-1);
}
}
Input: 3
Output: FACTORIAL IS : 6
The time complexity of the code is O(n).
The space complexity of the code is O(n), as we use a stack for storing each recursive call.This is the working of the recursion.
Now let’s understand how the recursive functions use the stack.
There is a special notation named the call stack which is used by the recursive functions each time it calls itself. Whenever the recursive function calls itself, the memory is allocated to the called function and placed on the top of the stack. Whenever the base condition of the recursive approach is reached, the function returns the value and de-allocation of memory from the stack and this process continues till the stack gets empty. Let’s understand the allocation of the memory for the called functions with the above-mentioned factorial example.
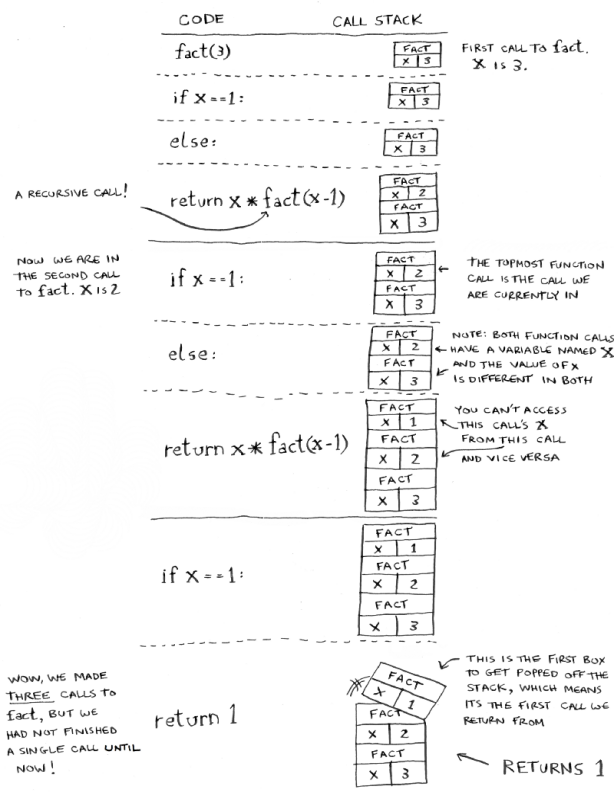
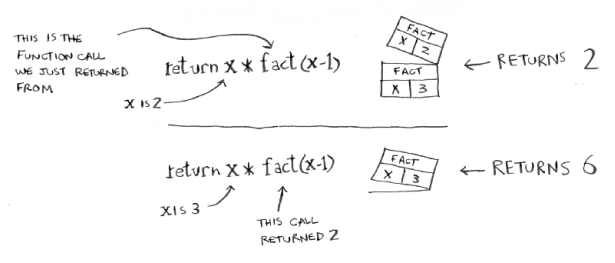
This is a clear explanation of how the memory is allocated for the function calls in the stack memory.
CONCLUSION
That’s it from this tutorial. Hope you guys found It interesting. We have understood the basic definition of recursion, some basic properties needed to be possessed by the recursive function, advantages and disadvantages of the recursion, differences between the recursion and the iteration, the working of the recursion, and how the memory is allocated for the called functions in the stack memory using recursion. Happy coding!

